Investigations on n-Spheres
The Wikipedia articles \(n\)-sphere and Volume of an \(n\)-ball and Volume of a unit sphere are not great references on the basic formulae because all the information is spread out among them in un-useful ways. I went to write my own reference… but then I got annoyed by the shape of the formulae themselves, with their strange Gamma functions and unintuitive \(\sqrt{\pi}\) factors, so I starting trying to refactor them. It didn’t all fall into place, unfortunately, but there were some discoveries that I found interesting (which are probably out there in the literature, or not, I don’t know). I thought I’d post it anyway because I still feel like there’s something here that I’m grasping around for and I’d like to save the progress I made.
(After posting this I made some edits and decided to split it in two, so a lot of the stuff on factorials and their interpretation is now in the sequel, Factorials Integrals and and √π.)
1. Measures of Spheres
Here are the volumes and surface areas of \(n\)-spheres \(S^n\) for the first few \(n\), as a function of the radius \(r\) (which I will sometimes omit if it’s not useful, later on):
\[\begin{aligned} S_0 &= 2 & V_1 &= 2r \\ S_1 &= 2 \pi r & V_2 &= \pi r^2 \\ S_2 &= 4 \pi r^2 & V_3 &= \frac{4}{3} \pi r^3 \\ S_3 &= 2 \pi^2 r^3 & V_4 &= \frac{1}{2} \pi^2 r^4 \\ S_4 &= \frac{8}{3} \pi^2 r^4 & V_5 &= \frac{8}{15} \pi^2 r^5 \\ \end{aligned}\]Here \(S_{n}\) is a surface area of the \(n\)-sphere of radius \(r\) (also called \(S^n\), with a superscript) and \(V_n\) is the volume of the \(n\)-ball \(B^n\) which is the interior of \(S_{n-1}\).I don’t really care for the “sphere” vs “ball” distinction; I like to just say they’re the area and volume of the same sphere. So most of the time I will not use the word ball.
\(S^0\) is a pair of \(0\)-dimensional points, since there are two points on a line a distance \(r\) from a single point, with surface “area” \(S_0 = 2\), and its volume is \(V_1 = 2r\) since it is a line segment of length \(2r\). \(S^1\) is a circle with surface area \(S_1 = 2\pi r\) and volume \(V_2\). The numbers refer to the dimensionality of the object, which is why they’re off-by-one for the surface areas vs. volumes: the two-dimensional disc has a one-dimensional boundary, etc. I’ve always found this a bit weird and confusing but there you go. So \(S^2(r)\) refers to a two-dimensional sphere, whose surface area is \(S_2(r) = 4 \pi r^2\) and whose volume is \(V_3(r) = \frac{4}{3} \pi r^3\).
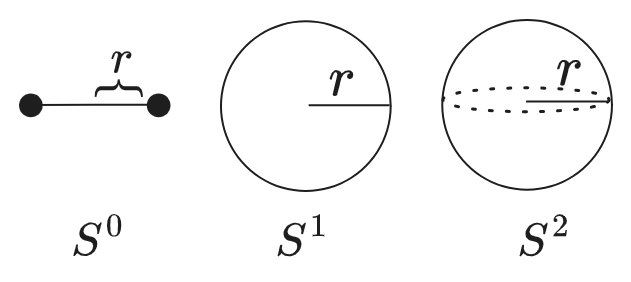
Wikipedia also talks about a \(V_0\), a single point, which would be the interior of a \((-1)\)-sphere, whatever that means. That seems dumb: there are no points in a \(0\)-dimensional space that are a distance \(r\) from anything. One argument to keep it around, maybe, is that it does seem to respect the same recurrence relation as the others. Maybe it is kinda implying that \(N\)-spheres are products of smaller-dimensional spheres, and, as with \(0!=1,\) the products start at \(1\)? I dunno.1
Here’s the general form of the areas and volumes, as written on Wikipedia:
\[\begin{aligned} S_{n-1} &= \frac{2 \pi^{n/2}}{\Gamma(\frac{n}{2})} r^{n-1} & V_n &= \frac{\pi^{n/2}}{\Gamma(\frac{n}{2} + 1)} r^n \\ \end{aligned}\]I have trouble thinking in terms of \(\Gamma\) functions so here they are written in terms of \(n! = \Gamma(n+1)\); we’ll just let the factorial be defined on non-integers in the same way that \(\Gamma\) is:
\[\begin{aligned} S_{n-1} &= \frac{2 \pi^{n/2}}{(\frac{n}{2}-1)!} r^{n-1} & V_n &= \frac{\pi^{n/2}}{(\frac{n}{2})!} r^n \\ \end{aligned}\]And even that for is a bit misleading, though. The factorials should really be thought of as having the same argument, and there’s just an extra factor of \(n\) canceling it out in the \(S_{n-1}\) formula.
\[\begin{aligned} S_{n-1} &= n \frac{\pi^{n/2}}{(\frac{n}{2})!} r^{n-1} & V_n &= \frac{\pi^{n/2}}{(\frac{n}{2})!} r^n \\ \end{aligned}\]That’s better. The factor of \(n\) is simplest because it just reflects the fact that \(\p_r V_n(r) = S_{n-1}\), because the boundary of a ball is the derivative of its volume with respect to radius (as it has to be). So \(V_n(r) = V_n r^n\) then \(S_{n-1}(r) = \p_r V_n(r) = n V_n r^{n-1}\).
But there’s something annoying about these formulas. The main problem is how they appear to have half-integer powers of \(\pi\) for odd \(n\), but they actually don’t, because the half-integer factorial also has a factor of \(\sqrt{\pi}\), eg \((\frac{1}{2})! = \frac{\sqrt{\pi}}{2}\), and the two cancel out.2 The other nuisance is that they just don’t see obvious at all: why are these the areas/volumes of \(n\)-spheres? Surely there is a more intuitive form?
There are also some recurrence relationships between the \(S\) and \(V\) formulas. The easy one is
\[S_{n-1}(r) = \p V_n(r)/\p r\]Which is obvious (and true for any figure, for a suitable definition of “radius”). But then there’s also stuff like
\[S_{n+1}(r) \? (2 \pi r) V_n(r)\]Which I don’t find especally helpful. What am I supposed to make of that? A sphere is the product of a circle and a line segment? I don’t understand why and I can’t really visualize what it means. Well: apparently it’s because e.g. the sphere’s surface area is the same as that of a (uncapped) cylinder of height \(2 r\) and radius \(r\) (\(2 \pi r \times 2r = 4 \pi r^2\)). But it’s very hard to see intuitively why that should be the case, or why it would generalize.3
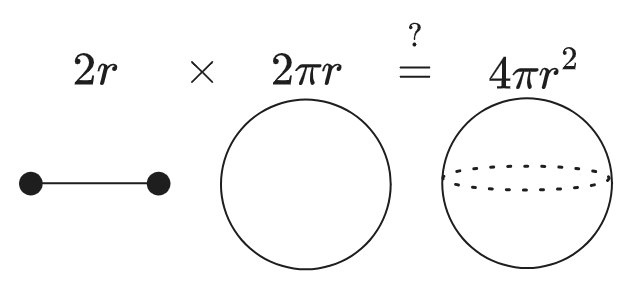
Here’s a chart of various relations. I’ve also walked it into the negatives a bit because that’s kinda fun to think about, although I won’t be looking into that here…

There are other recurrence-like relationships that deserve explanation but which I don’t think I understand still. For instance, why is \(S_2(r) = 4 V_1(r)\) intuitively? How do you cover a sphere with four circles of the same radius? I have no idea. There is a 3b1b video about that particular identity, but I don’t feel satisfied with the explanation even after watching it: it is the sort of thing you have to show, not the sort of thing you see; none of the explanations make it obvious. I would like to have a way of seeing this relationship as completely natural, but that seems very hard to find. Whatever it is, it also has to explain why \(S_3\) and \(V_3\) differ by a factor proportional to \(\pi\) while \(S_2\) and \(V_2\) do not, and right now I can’t even imagine a kind of argument that could explain that.
To make more sense of all this I’m just going to play around with formulas until something pops out.
2. Derivations
Here’s a lot of work to derive the formulas for \(S_n\) and \(V_n\) in various ways.
The most straightforward way is to compute a big integral: to find the area/volume of an \(n\)_sphere, integrate over its surface/interior. This is fairly straightforward, if tedious.
Each \(n\)-sphere is parameterizable by one angle \(\theta \in (0, 2\pi)\) and then \(n-1\) angles \(\phi_i \in (0, \pi)\), plus a \(r \in (0, R)\) if you want to get the volume of the interior (see here). Basically the first \((0, 2\pi)\) range is for the initial circle (picture the equator of a sphere), and then you repeatedly add polar angles akin to a sphere’s \(\phi \in (0, \pi)\) which adds up a bunch of circles of varying radii. Then the formulas are what you get when you integrate over the whole surface, like
\[S_2(r) = \int_0^{2 \pi} \int_0^{\pi} r^2 \sin (\phi) \d \phi \d \theta = 4\pi r^2\]Higher dimensions have more and more copies of \(\sin^k (\phi_i)\) on each successive angular variable, and thankfully, the big multivariable integral splits into a product into a product of single-variable integrals because none of the variables are shared. For instance
\[\begin{aligned} S_3(r) &=\int_0^\pi \int_0^\pi \int_0^{2\pi} r^3 \sin^2 (\phi_2) \sin( \phi_1) \d \phi_1 \d \phi_2 \d \theta \\ &= \big[ \int_0^\pi r \sin^2 (\phi_2) \d \phi_2 \big] \big[ \int_0^\pi r \sin (\phi_1) \ d \phi_1 \big] \big[ \int_0^{2\pi} r \d \theta \big] \\ &= [\frac{\pi}{2} r] [2 r] [2 \pi r] \\ &= 2 \pi^2 r^3 \end{aligned}\]and when you work out the general case you get the formulas for \(S_n\) (and \(V_n\) if you integrate over \(r\) as well).
In particular, the source of the “every other term has a factor of \(\pi\)” phenomenon is that \(\int_0^{\pi/2} \sin^k (\theta) d \theta\) gives a factor of \(\pi\) for even \(k\) and not for odd. The reason can be seen by inspecting \(\sin^2 \theta = \frac{1}{2}(1 - \cos 2 \theta)\) while \(\sin^3 \theta = \sin \theta (1 - \cos^2 \theta) = \p_\theta (-\cos \theta + \frac{1}{3} \cos^3 \theta)\), so the bare \(1\) on the even sine powers becomes a factor of \(\pi\).
This all assumes you already know the area element for the surface, which I skipped above. Coming up with it is a bit annoying if you only know the standard multivariable approach, with a big Jacobian determinant (hate that name) of the parameterization. A better way to think about it is this:
First consider computing \(S_1 (r)\). The circumference of a circle is given by integrating its arc length, which is a one-dimensional curve subject to the condition that \(x^2 + y^2 = r^2\), that is, if \(x = r \cos \theta\), then \(y = \sqrt{r^2 - x^2} = r \sin \theta\). So we add up \(\| (dx, dy) \| = \| (r \cos \theta, r \sin \theta) \| = r \d \theta\) over the whole thing:
\[\begin{aligned} S_1(r) &= \int_{S_1(r)} \| dS_1(r) \| \\ &= \int_{x^2 + y^2 = r^2} \| (dx, dy) \| \\ &= \int_{x^2 + y^2 = r^2} \sqrt{dx^2 + dy^2} \\ &= \int_{\theta = 0}^{2 \pi} \sqrt{(-r \sin (\theta) \d\theta )^2 + (r \cos (\theta) \d \theta)^2} \\ &= \int_0^{2\pi} r \d \theta \\ &= 2 \pi r \end{aligned}\]To compute \(S_2(r)\), which is the level set of \(x^2 + y^2 + z^2 = r^2\), we can parse it as integrating a “circle” as well: it’s the solutions to the constraint
\[\rho^2 + z^2 = r^2\]Where \(\rho = \sqrt{r^2 - z^2}\) is the radius of the circle at height \(z\). So the contribution to the area at each time is the same circular length element, times the circumference \(S_1(\rho)\) of this circle. But we can parameterize these variables by another angle \(\phi \in (0, \pi)\): \(z = -r \cos \phi\) for \(\phi \in (0, \pi)\) and then \(\rho = r \sin \phi\):
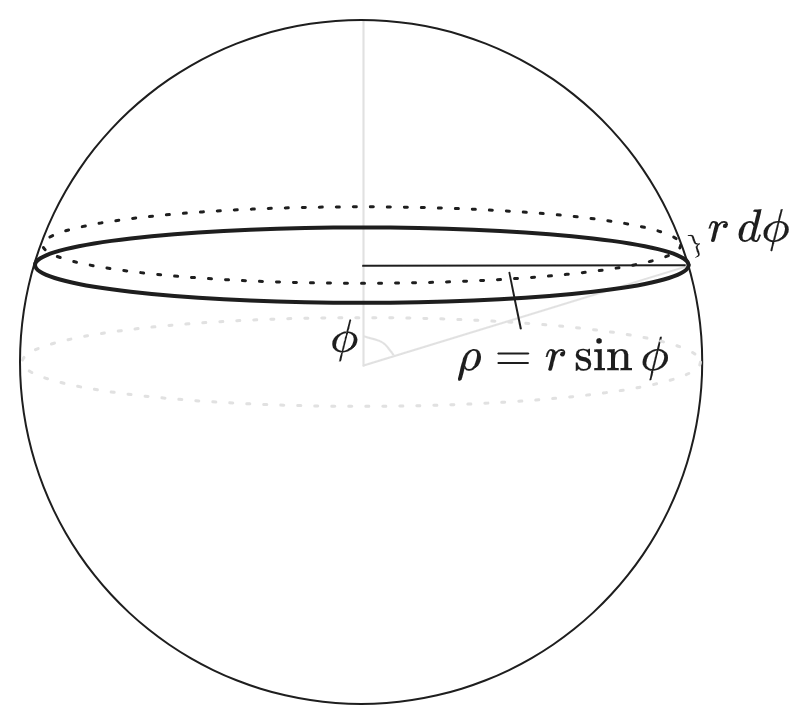
Each area contribution is \(S_1(r \sin \phi) \times r \d \phi\) for each differential \(d \phi\):
\[\begin{aligned} S_2(r) &= \int_0^\pi S_1(r \sin \phi) r \d \phi \\ &= \int_0^\pi (2 \pi r \sin \phi) r \d \phi \\ &= 4 \pi r^2 \end{aligned}\]The nice thing about looking at it this way is that it’s clear how that it generalizes: each sphere \(S_n(r)\) is given by
\[S_n(r) = \int_0^\pi S_{n - 1}(r \sin \phi_n) r \d \phi_N\]And since the radial dependence of \(S_{N-1}\) is \(r^{n-1}\), we can factor out everything but the sine:
\[S_n(r) = S_{n - 1} r^n \int_0^\pi \sin^{n-1} \phi_{n}\d \phi_n\]Which gives a recurrence when we start from the base case of \(S_0(r) = 2\). IMO this is the simplest way of thinking of how the recurrence works and why each term is the integral of a higher power of \(\sin \phi\).
In light of this it is clear that the fact that the first angle has a different range, \(\theta \in (0, 2\pi)\), is just a fluke. To make the pattern hold, it should really be thought of as being multiplied by \(S_0 = 2\) at each point.
\[\begin{aligned} S_1(r) &= \int_0^\pi S_0(r \sin \theta) \times (r \d \phi) \\ &= \int_0^\pi 2 r \d \phi \\ &= 2 \pi r \end{aligned}\]That is: the circle \(S^1(r)\)’s interior is the sum of the lengths of horizontal chords of length \(\rho = 2 r \sin \theta\), which are each copies of \(S_0(r)\), and its surface area is the sum of the surface “areas” of those. (Of course, you could surely modify the other integrals to be in \((0, 2\pi)\) as well, with appropriate factors of \(2^{-n}\). But this seems more elegant to me).
Similarly, for volume: the volume \(V_n\) is given by the integral of \(V_{n-1}\), but now the integrand is \(dz = R \sin \phi_n \d \phi_n\). For \(n = 1\), where we’ll go ahead and parameterize the circle with \(\phi \in (0, \pi)\) (and note, there’s a negative sign because this integrates \(dz\) starting from the top of the circle instead of the bottom):
\[\begin{aligned} V_2(r) &= \int_{-r}^r V_1(\sqrt{r^2 - z^2}) \d z \\ &= \int_{0}^{\pi} V_1(r \sin \phi) \d (-r \cos \phi) \\ &= \int_0^\pi (2 r \sin \phi) (r \sin \phi \d \phi) \\ &= 2 r^2 \int_0^\pi \sin^2 (\phi) \d \phi \\ &= 2 r^2 \int_0^\pi (\frac{1}{2} - \frac{1}{2} \cos 2 \phi) \d \phi \\ &= 2 r^2 (\frac{1}{2} \phi - \frac{1}{4} \sin 2 \phi) \big|_0^\pi \\ &= \pi r^2 \end{aligned}\]
Note that there are two more \(\sin \phi\)s in the integral compared to the \(S_1\) integral. One comes from the fact that we used the volume of \(S_0(r \sin \phi)\). The other is from the integrand being \(dz = r \sin (\phi) \d \phi\) instead of just \(r \d \phi\). This may be interpreted as being produced by a wedge product: we could still integrate in \(r \d \phi\), but since we are computing an area, we need to use \(V_0(r \sin \phi) \^ r \d \phi\), and that interacts only with the orthogonal component, which is \(dz = r \sin \phi \d \phi\).
And in general:4
\[\begin{aligned} V_n(r) &= \int_{-r}^r V_{n-1}(\sqrt{r^2 - z^2}) \d z \\ &=\int_{\pi}^0 V_{n-1}(r \sin \phi_n) \d (r \cos \phi_n) \\ &=\int_0^\pi V_{n-1}(r \sin \phi_n) \times (r \sin (\phi_n) \d \phi_n) \\ &= V_{n-1} r^n \int_0^\pi \sin^{n} (\phi_n) \d \phi_n \\ \end{aligned}\]Once again, the extra factor of \(\sin \phi_n\) shows up because since we are computing a volume we need to multiply the area of the \(S^{n-1}\) circle by the orthogonal part of \(r \d \phi_n\), which is \(dz\).
\[V_n(r) = \int_0^\pi V_{n-1}(r \sin \phi_n) \^ r \d \phi = \int_0^\pi V_{n-1}(r \sin \phi_n) dz\]3. Polyspherical Integrals
In fact, this process can be generalized quite a bit, into what I would call “polyspherical integrals”, since it’s related to something apparently called polyspherical coordinates—although I think my version makes a lot more sense than what’s on there.
What’s really going on when we compute \(V_n\) from \(V_{n-1}\) is that, for every element on the line \(z \in (-r, r)\), we are accumulating a copy of \(V_{n-1}\). But \((-r, r)\) is itself a copy of \(V_1\). At each point so the integral really has the form
\[V_n(r) = \int_0^{\pi/2} V_{n-1}(r \sin \phi_n) d V_1(z)\]This can be done with more than just \(n = (n-1) \oplus (1)\). In fact an \(n = p + q\) sphere can be seen as a “product” of a \(p\)-sphere and a \(q\)-sphere, as follows:
Consider the constraint equation for \(S^{p+q}\)
\[\underbrace{x^2_1 + x^2_2 + x_p^2}_{p} + \ldots + \underbrace{x^2_{p+1} + x^2_{p+2} + \ldots x^2_{p+q}}_{q} = r^2\]This can be seen as describing two spheres whose radii obey \(r_p^2 + r_q^2 = r^2\):
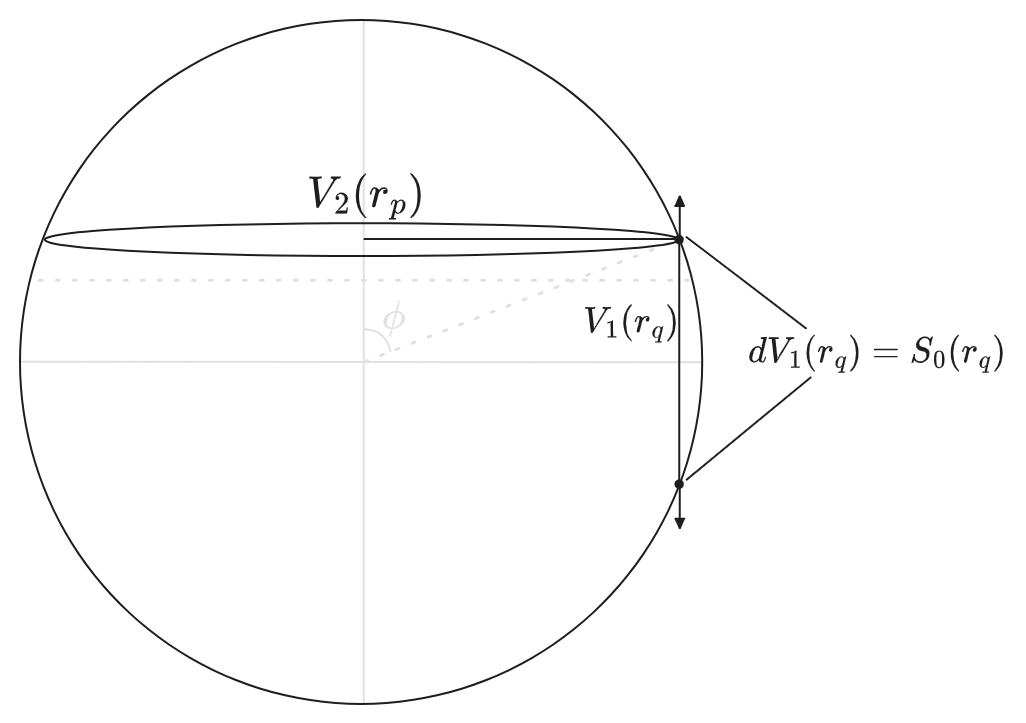
\[\| \b{x}_p \|^2 + \| \b{x}\|_q^2 = r_p^2 + r_q^2 = r^2\]To compute \(V_{p+q}\), then, we can add up: \(V_q(r) = \int_0^r \p_{r_q} V_q(r_q) \d r_q = \int_0^r dV_q(r_q)\) describes the volume of \(V_q\), and then for each radius \(r_q\), there is dual radius \(r_p = \sqrt{r^2 - r_q^2}\) which contributes a factor of \(V_p(r_p)\):
\[\begin{aligned} V_{p+q} &= \int_0^{r} V_{p}(r_p) dV_q(r_q) \\ &= \int_0^r V_p(\sqrt{r^2 - r_q^2}) S_{q-1}(r_q) dr_q \\ &= \int_0^{\pi/2} V_p(r \sin \phi) S_{q-1}(r \cos \phi) r \sin \phi \d \phi \end{aligned}\]For example: the volume of a sphere \(V_3\) may be computed with \(p=2, q=1\)
\[\begin{aligned} V_3(r) &= \int_0^{r_q} V_2(r_p) dV_1(r_q) \\ &= \int_0^{\pi/2} [\pi r^2 \sin^2 \phi] d[- 2 r \cos \phi] \\ &= 2 \pi r^3 \int_0^{\pi/2} \sin^3 \phi \d \phi \\ &= 2 \pi r^3 [- \cos \phi + \frac{1}{3} \cos^3 \phi]\big|_0^{\pi/2} \\ &= \frac{4}{3} \pi r^3 \\ \end{aligned}\]Which corresponds to summing up a circle for each value of \(z = r_q\), as above. (Note, the reason the the integration bounds are \((0, \pi/2)\) is because we’re integrating over each possible radius inside \(V_1(r_q)\), and at each radius there is a pair of points, with “volume” \(S_0(r_q) = 2\). The factor of \(2\) takes care of adding the upper and lower hemispheres together.)
Or it can be created with \(p=1, q=2\), which is a \(2r_p\)-length line segment times each ring of a circle with radius \(r_q\):
\[\begin{aligned} V_3(r) &= \int_0^{r} V_1(r_q) dV_2 (r_p) \\ &= \int_0^{\pi/2} [2 r \sin \phi] d [\pi r^2 \cos^2 \phi] \\ &= 4 \pi r^3 \int_0^{\pi/2} (\sin \phi) (-\cos \phi \sin \phi) \d \phi \\ &= 4 \pi r^3 [-\frac{1}{3} \sin^3 \phi] \big|_0^{\pi/2} \\ &= \frac{4}{3} \pi r^3 \end{aligned}\]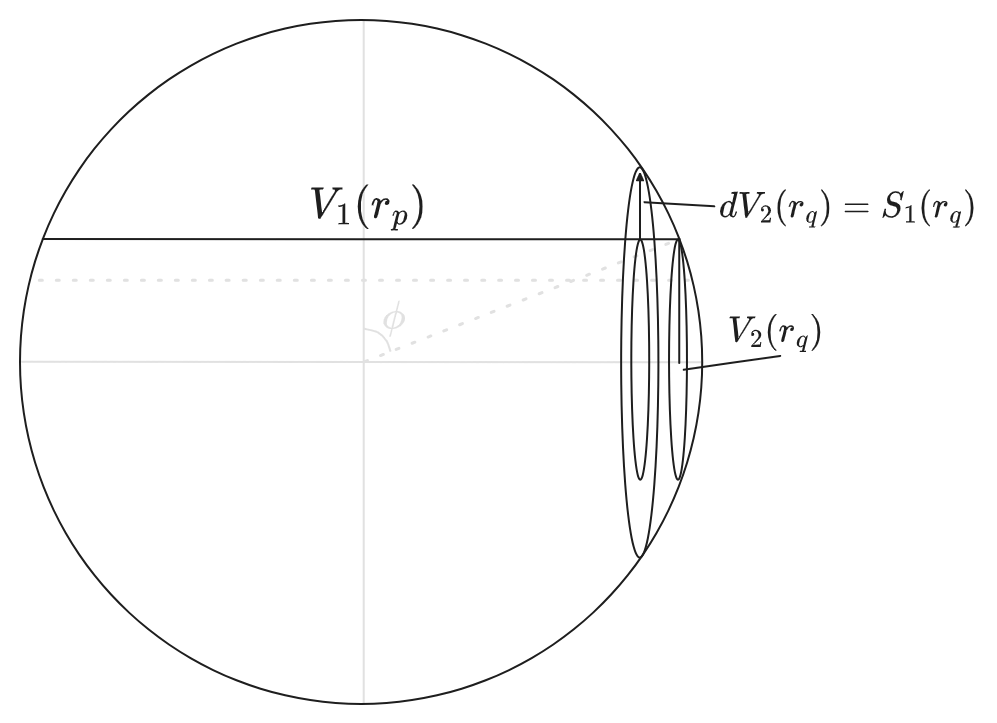
The general case for the volume of a \((p+q)\)-sphere is
\[V_{p+q}(r) = \int_0^{r_q} V_p(r_q) dV_q(r_p)\]And I’ll wwork it out explicitly to make sure I am not totally lost.
\[\begin{aligned} V_{p+q}(r) &= \int_0^{r_q} V_p(r_q) dV_q(r_p) \\ &= \int_0^{\pi/2} \frac{\pi^{p/2} (r \sin \phi)^{p} }{(\frac{p}{2})!}d \big[ \frac{\pi^{q/2} (r \cos \phi)^{q} }{(\frac{q}{2})!} \big] \\ &= \frac{\pi^{(p+q)/2} }{(\frac{p}{2})! (\frac{q}{2}-1)!}r^{p+q} \times 2 \int_0^{\pi/2} \sin^p \phi \cos^{q-1} \phi \sin \phi \d \phi \end{aligned}\]We could hack that out manually, but it’s easier to defer to the Wikipedia for beta functions. With \(z_1 = \frac{p}{2}+1\) and \(z_2 = \frac{q}{2}\) we get
\[\begin{aligned} 2 \int_0^{\pi/2} \sin^p \phi \cos^{q-1} \phi \sin \phi \d \phi &= 2 \int_0^{\pi/2} \sin^{2z_1-1} \phi \cos^{2z_2-1} \d \phi \\ &= \beta(z_1, z_2) \\ &= \frac{\Gamma(z_1) \Gamma(z_2)}{\Gamma(z_1 + z_2)} \\ &= \frac{(\frac{p}{2})! (\frac{q}{2}-1)!}{(\frac{p+q}{2})!} \\ V_{p+q}(r) &=\frac{\pi^{(p+q)/2} }{(\frac{p}{2})! (\frac{q}{2}-1)!}r^{p+q} \big[ \frac{(\frac{p}{2})! (\frac{q}{2}-1)!}{(\frac{p+q}{2})!} \big] \\ &= \frac{\pi^{(p+q)/2} }{(\frac{p+q}{2})!} r^{p+q} \end{aligned}\]As expected.
The equivalent integral for surface area is given by \(\p_r\) times this, which is a mess, or it’s just given the integral of both surfaces areas times \(r d \phi\), via a similar \(\beta(p/2, q/2)\) argument:
\[\begin{aligned} S_{p+q-1}(r) &= \int_0^r S_{p-1}(r_p) S_{q-1}(r_q) r \d \phi \\ &= \int_0^{\pi/2} S_{p-1}(r \sin \phi) S_{q-1}(r \cos \phi) r \d \phi \\ &= \frac{2 \pi^{(p+q)/2}}{(\frac{p+q}{2}-1)!} r^{p+q-1} \end{aligned}\]Which of course could also be written
\[\p_r V_{p+q} = \int_0^r \p_{r_p} V_{p}(r_p) \p_{r_q} V_q(r_q) r \d \phi\]I find
\[\begin{aligned} V_{p+q} &= \int_0^{r} V_p(r_p) dV_q(r_q) \\ \end{aligned}\]and to a lesser extent
\[S_{p+q-1} = \int_0^r S_{p-1}(r_p) S_{q-1}(r_q) r d \phi\]To be the most agreeable interpretations so far. They at least, in a sense, construct larger spheres out of smaller ones in a way that makes the recurrences make a bit of sense. The sense in which \(S^3 = S^2 \times S^1\), for instance, is an integral of this sort. These integrals may also be seen as a sort of convolution: since \(\sin \phi = \cos (\frac{\pi}{2}-\phi)\), it effectively looks like an integral \(\int_0^{\pi/2} f(\pi/2-\phi) g(\phi) \d \phi \? f(\phi) \ast g(\phi)\). Maybe that’s the sense in which this is “spherical convolution”, and then there’s a Fourier-like space in which these integrals are literally something like “multiplication”?
One other thought I had in the middle of this: I can sorta see why this leads to a new factor of \(\pi\) for only even \(n\). Consider something like \(w^2 + x^2 + y^2 + z^2 = r^2\). When we go to integrate the volume of this, the integral can be factored as two convolved circles, each of which has a factor of \(\pi\), meaning the volume ought in some sense to have a factor of \(\pi^2\). A sphere times a line segment then might get \(\pi^2\) because it can be written as a circle times a circle. But a circle times a line segment only has one factor of \(\pi\) no matter how you split it up. Basically, it takes a pair of dimensions to produce each \(\pi\), so for every pair of dimensions you get another factor.
Anyway. Let’s move on. I want to look more closely at where the factorials come from.
4. Spherical Tetrahedrons
Another direction of investigation is to compare \(n\)-spheres to \(n\)-tetrahedrons.
Recall the relationship between \(S_{n-1}\) and \(V_n\):
\[V_n(r) = \frac{r}{n} S_{n-1}(r)\]This factor of \(n\) is not specific to spheres; it shows up for any formula that’s proportional to \(r^n\). For example it is also there in triangles/tetrahedrons/their \(n\)-dimensional generalization, \(n\)-simplexes. If the base of an \(n\)-simplex \(P = (p_0 p_1 \ldots p_n)\) is an \((n-1)\)-simplex with area \(A\) and the “height” \(h\) is the distance from \(B\) to the final point, then
\[\vol(P) = \frac{1}{n} h B\]Which is the \(n\)-dimensional analogue of a triangle’s \(A = \frac{1}{2} \text{base} \times \text{height}\). For instance a tetrahedron has volume \(V = \frac{1}{3} B h\).
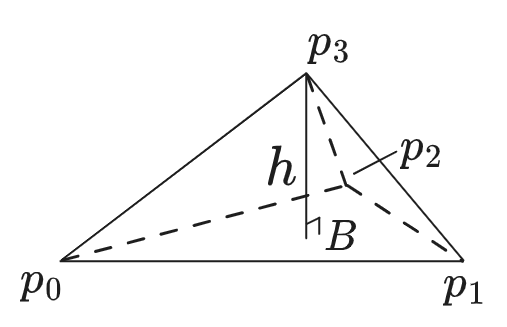
More generally, if
\[A = \frac{1}{(n-1)!} (p_0 \^ p_1 \^ \ldots \^ p_{n-1})\]is the “area” (that is, \((n-1)\)-volume) of the base as a multivector, then
\[\vol(P) = A \^ \frac{1}{n} p_n = \frac{1}{n!} [p_0 \^ p_1 \^ \ldots p_{n-1} \^ p_n]\]The height \(h\) happens to be the orthogonal component of \(p_n\) off of \(A\), which is why the formula factors that way if you already know it.
In the case of a tetrahedron, the volume can be written in terms of the base \(a\) and height \(b\) of one of its faces, times the height \(c\) from that face:
\[V = \frac{1}{3} (\frac{1}{2} ab) c = \frac{1}{3!} abc\]Which is where the factorial comes from: you can keep chopping off one point at a time, picking up factor of \(1/n \times 1/(n-1) \times \ldots = 1/n!\).
A cone has a similar formula. For a three-dimensional cone with flat base the volume is still \(V = \frac{1}{3} A h\). This may be seen by imagining it to be created out of an infinite number of tiny tetrahedrons or any of various other arguments. One is: both tetrahedrons and cones have the property that they are self-similar as you move along the \(h\) axis. If you double the height \(h \ra 2h\), each dimension of the base also doubles, giving \(B \ra 2^2 B\). So, as a function of height, \(B(h) = B h^2\). The volume, then, is \(V = \int B(h) \d h = \int B h^2 \d h = \frac{1}{3} B(h) h^3 = \frac{1}{3} B h\). The self-similarity along \(h\) fixes the \(h\)-dependence of the volume to be \(\frac{1}{3} h\) (or \(1/n\) in general).
Now consider a different kind of cone: a slice of a sphere, which has a rounded base instead of a flat one (a spherical cap). Now every point on the base is the same distance \(r\) from the vertex. The area of the face can be thought of as being a fraction of the surface of a sphere with the same radius. If the fraction is \(k\), then the area of the base is \(k (4 \pi r^2) = \Omega r^2\), where \(\Omega = 4\pi k\) is the solid angle at the vertex. Just as a one-dimensional angle \(\theta \in (0, 2\pi)\) measures the amount of circumference of a unit circle swept out between two directions, a solid angle is the portion of the area of a unit sphere swept out by some volume. Hence \(\Omega\) takes values \(\in (0, 4\pi)\), since \(4\pi\) is the surface area of a unit sphere (with units of “steradians”), and the area of the base of the curved cone of radius \(r\) and solid angle \(\Omega\) is
\[A = \frac{\Omega}{4\pi} (4 \pi r^2) = \Omega r^2\]The volume is the same fraction of the sphere’s overall volume:
\[V = \frac{\Omega}{4 \pi} V_3(r) = \frac{\Omega}{4\pi} (\frac{4}{3} \pi r^3) = \frac{1}{3} \Omega r^3 = \frac{1}{3} A r\]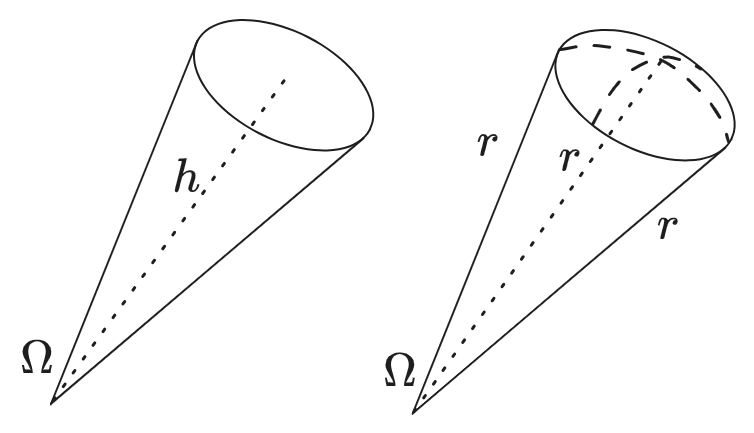
Which once again is one-third of the area of the base, times the height, exactly the same as the flat cone. It’s for the same reason as before: the curved cone is still self-similar along its axis, hence has the same radial/”height” dependence. This is analogous to how in two dimensions the area of an arc of a circle with angle \(\theta\) is given by \(\int_0^{\theta} \int_0^r r \d r \d \theta = \frac{1}{2} \theta r^2\) (see my other post on angles for more on this). An arc of a circle is a sort of triangle, and a spherical cone is a sort of circular pyramid? And a sphere is a cone with angle \(\Omega = 4 \pi\).
A cone is not, however, really the circular equivalent of a tetrahedron. That would be something like this:
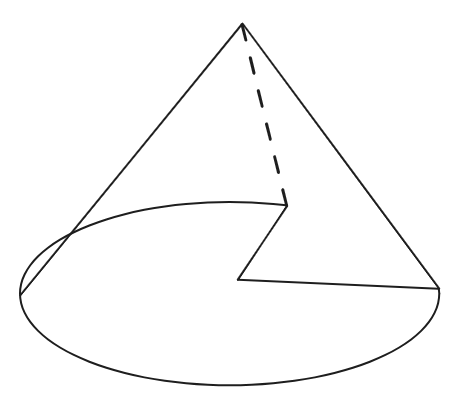
Since it needs to be a fraction of a solid angle and then have its base be a fraction of a regular angle as well. Otherwise the base of the cone doesn’t an obvious \(\frac{1}{2} bh\) formula like a triangle. This is (presumably!) why the formulas for the volumes/areas of \(n\)-spheres do not have \(\frac{1}{n!}\) in front of them (since they have \(\frac{1}{(\frac{n}{2})!}\) instead…).
The area of the base of a cone is \(\Omega r^2\), but it would be nice to see that in terms of numbers we know how to actually measure. Here’s a diagram:
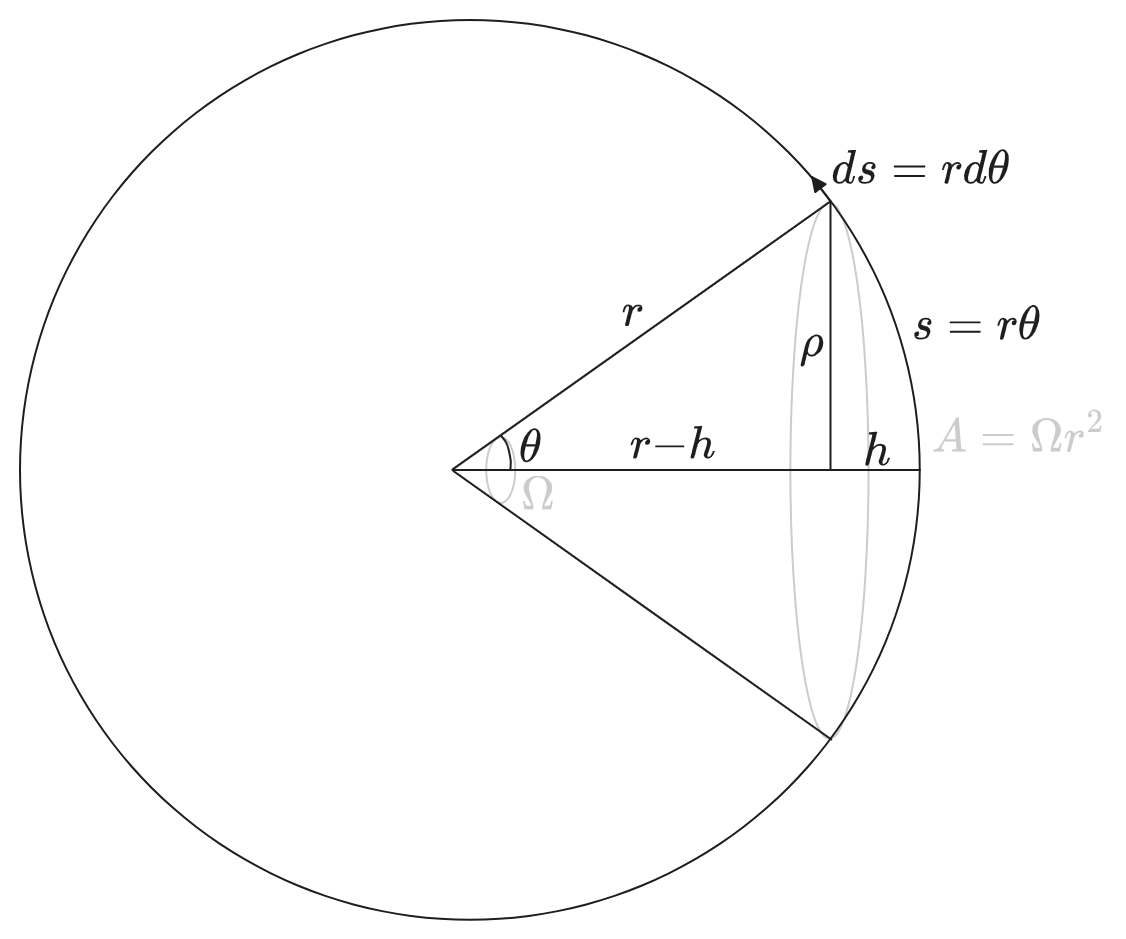
The quickest way to get the answer is to use the fact we mentioned a long time ago, that the surface area of a sphere is the same as its projection onto a cylinder of radius \(2 \pi r\) and height \(2r\). But I still don’t find that very intuitive (or easy to generalize). So instead we’ll do it by integrating: each differential \(ds = r d \theta\) contributes \(dA = (2 \pi \rho) ds = 2 \pi r^2 \sin \theta d \theta\) to the area of the cap, giving
\[\begin{aligned} A &= \int_0^{\theta} 2 \pi r^2 \sin \theta \d \theta \\ &= 2 \pi r^2 (1 - \cos \theta)\\ &= 2 \pi r h \\ \Omega r^2 &= 4 \pi r^2 \sin^2 \frac{\theta}{2} \\ \Omega &= 4\pi \sin^2 \frac{\theta}{2} \\ \end{aligned}\]Anyway, whatever this area is, it’s not a \(\frac{1}{2} bh\) formula like a tetrahedron’s base.
The reason I’m talking about this at all is that I’m hoping to locate something like that might justify the \(\pi^{n/2} / (\frac{n}{2})!\) in the \(n\)-sphere’s formula. We saw that the \(1/n!\) in the \(n\)-simplex comes from being recursively self-similar. Does the \((n/2)!\) come from being self-similar in some other way?
Here’s an idea that didn’t work: what if the above area formula was that of a circle? Well.
Incidentally, we’ve seen elsewhere (here and in the sequel article on factorials), half-integer factorials are almost just integer factorials times an oscillating factor of \(\pi^{\pm 1/2}\):
\[(\frac{n}{2})! (\frac{n-1}{2})! = \frac{n!}{2^{n}} \sqrt{\pi}\]So in a way the half-integer factorial serves only to make the \(\pi\) factors work out. Maybe we should see how \(V_n\) and \(S_{n-1}\) look with explicit factors of \(\frac{1}{n!}\) in front:
\[\begin{aligned} V_n(r) &= \frac{\pi^{n/2}}{(\frac{n}{2})!} r^n \\ &= \frac{r^{n}}{n!} \times \big[ 2^n \pi^{(n-1)/2}(\frac{n-1}{2})!\big] \\ S_{n-1}(r) &= \frac{2 \pi^{n/2}}{(\frac{n}{2}-1)!} r^n \\ &= \frac{r^{n-1}}{(n-1)!}\times \big[ 2^{n} \pi^{(n-1)/2}(\frac{n-1}{2})! \big] \end{aligned}\]I almost prefer that. Even though the big bracketed term is awkward, at least the overall shape of the expression makes some sense. In fact, if you think of the \(2^n\) as accounting for how a sphere can be subdivided into \(2^3 = 8\) equal octants, then the formula really says: the area of an octant is
\[\frac{S_{n-1}}{2^n} = \frac{ \pi^{(n-1)/2}(\frac{n-1}{2})!} {(n-1)!}\]Which is, at least, the area of a spherical \((n-1)\)-triangle, with a formula that looks kinda like the formula for \((n-1)\)-triangles. Suppose we write \(T_{n-1} = S^{n-1}/2^n\) for one of these triangles (e.g. \(T_2\) is one eighth of a sphere’s surface, a spherical triangle with three angles of \(\pi/2\))
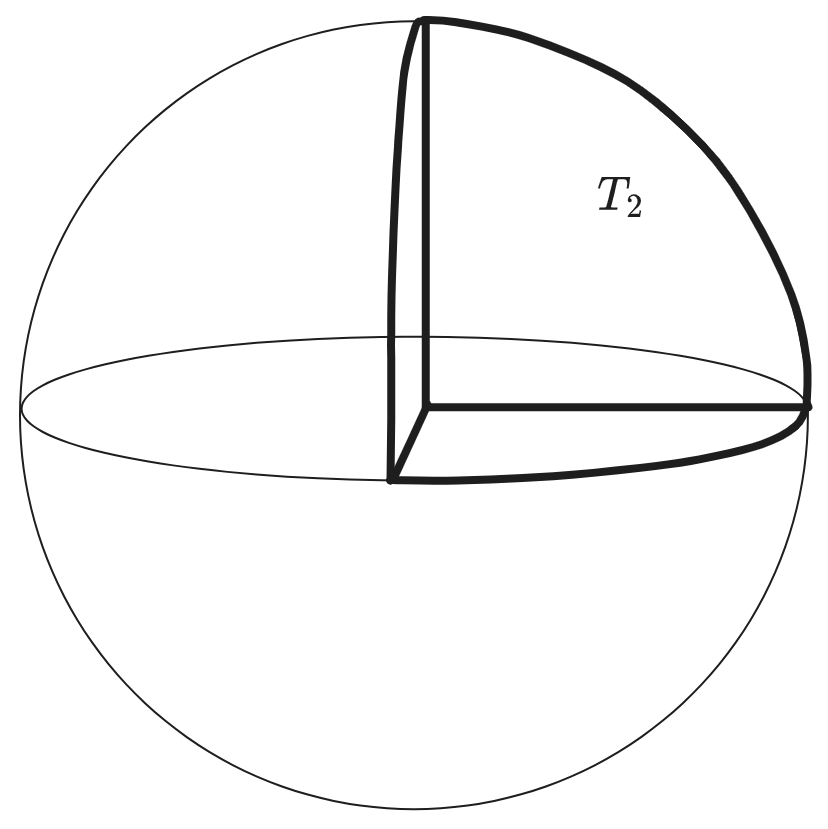
Then the \(V = \frac{1}{n} A h\)-type formula is
\[\begin{aligned} T_{n} &= \frac{ \pi^{n/2}(\frac{n}{2})!} {n!} \\ &= \frac{1}{n} T_{n-1} \times [ \sqrt{\pi} \frac{(\frac{n}{2})!}{(\frac{n-1}{2})!} ] \end{aligned}\](where of course that factor is never actually a half-integer power of \(\pi\), because every other factorial term is \(\pi^{\pm 1/2}\).) I don’t know what it means, but at least it looks like something vaguely geometric. But I don’t know what else to do with it.
5. Half-dimensional Tetrahedrons?
One other interesting triangle-like relationship:
The volume of an even-dimensional sphere may be written in terms of \(k = n/2\) as
\[V_{2k} = \frac{\pi^k}{k!} r^{2k}\]Which we may rewrite as
\[V_{2k}(r) = \frac{(\pi r^2)^k}{k!}\]This is another interpretation of why \(V_n = V_2 V_{n-2}/(n/2)\) holds, by the way. It’s a derivative with respect to \(k\):
\[\p_k V_{2k}(r) = \frac{(\pi r^2)^{k-1}}{(k-1)!} = V_{2(k-1)}(r)\]If we think about this as being in units of \(s = \pi r^2\):
\[V_{2k}(s) = \frac{s^k}{k!}\]Which is curious! The even-dimensional spheres look like repeated integrations \(V_{2k}(s) = \int_0^{s} \int_0^{s} \ldots d^k s\). They’re not exactly products of circles (those are the toruses—the spheres are, I guess, \(1/k!\) fractions of them?), but they’re the polynomials of circles, whatever that means. And as such their volume formulas look like those of simplexes: it is the volume of a right-angled \(k\)-simplex whose side lengths are each \(\pi r^2\).
I don’t know what to make of that. Is there some perspective in which even-dimensional spheres are \(k\)-simplexes whose sides are circles? And odd-dimensional spheres are half-integer-dimensional simplexes? Do you get the odd-dimensional spheres by taking half-derivatives? Yikes.
6. Ending
The point of all this was to try to make some sense for myself of the fact that \(\sqrt{\pi}\)s are doing weird things in the formulas for \(N\)-spheres. I don’t think I really got to the bottom of it, but along the way I do think I settled some confusions about factorials for myself.
I’ve left all my notes here in case anyone (or me in the future) can see some connection that I’m missing. I really want to see some “natural” way for those formulas to show up: some geometric construction that has these properties:
- It clearly produces \(N\) spheres from \(N-1\) spheres
- It clearly involves a factor of \(\sqrt{\pi}\)
- And it’s clear where the oscillating factor of \(\sqrt{\pi}\) that cancels that one out is coming from.
I didn’t quite find that, but I guess that’s okay. I learned and wrote out a lot of other stuff on the way.
-
Another argument for including it: the intersection of the sphere \(S^2\) with a plane is a copy of \(S^1\) the intersection of \(S^1\) with a line is a copy of \(S^0\). I suppose the intersection of \(S^0\) with a point (or a line, for that matter) is a copy of \(S^{-1}\)? ↩
-
At the moment there’s a comment in the Wikipedia article about it—that was me, I added that as I was writing this. ↩
-
This corresponds to the fact that per unit height a sphere’s surface area is constant, so there really is one \(2\pi r\)’s sphere worth of area per \(2r\) worth of diameter. ↩
-
Incidentally, each \(\int_0^\pi \sin^n \phi \d \phi = \sqrt{\pi} \frac{(n/2-1/2)!}{(n/2)!}\) term gives the ratio \(V_n/V_{n-1}\) (these are apparently known as Wallis’ Integrals). ↩