Still more investigation into why \((-\frac{1}{2})! = \sqrt{\pi}\). Now we are circling in on the real question, which is: what could it possibly mean to take a permutation of a fractional number of elements?

At this point I am not recounting regular mathematics at all but instead just meandering around my own thoughts on the subject. Read on if that’s interesting to you, but be warned, this is more-or-less a stream of consciousness. If I find anything good I’ll summarize it later.

Previously:¹

• Investigations on n-Spheres
• Factorials as Multiplicative Integrals
• More on √π

---

1. An Interpolation of Spheres

A fruitful explanation for \(\Gamma(\frac{1}{2}) = (-\frac{1}{2})! = \sqrt{\pi}\) is going to be one that generalizes well: if we can come up with a reason why \(\sqrt{\pi}\) is the value, it should also give, at minimum, answers to why the other values of \(\Gamma\) are what they are. For example,

\[\Gamma(\frac{1}{4}) = (-\frac{3}{4})! = \sqrt{2 \varpi \sqrt{2 \pi}}\]

Where \(\varpi\) is the lemniscate constant. (We are not going to actually talk about the lemniscate itself, really, just the constant that comes from its area. Sorry for the misleading title.) Perhaps it could simplify some of the nightmarish expressions that are known for other values of \(\Gamma\) such as

\[\begin{aligned} \Gamma(\frac{1}{3}) &= 2^{7/9} \frac{\sqrt[3]{\pi K(\frac{\sqrt{3}-1}{2 \sqrt{2}})}}{\sqrt[12]{3}} \end{aligned}\]

where \(K(k) = \int_0^1 (1-t^2)^{-1/2} (1-k^2 t^2)^{-1/2} \d t\) is a certain type of elliptic integral. You can see some others on Wikipedia under Particular values of the Gamma function; notice that closed expressions are only known for a few of them. And really most of those are cheating a bit, because if you’re counting an elliptic integral (equivalently, an arithmetic-geometric mean) as a “closed expression”, you may as well count \(\Gamma(z) = \int_0^{\infty} z^{t-1} e^{-t} \d t\), which would be silly. So we’re not crossing our fingers for finding any closed forms here: probably \(\Gamma(x)\) can be regarded as the definition of many constants; who’s to say we shouldn’t be defining \(\pi\) as \(\Gamma(1/2)^2\) anyway? Still, we would like some simpler equations if possible.

So far the most compelling clue has been that the volume of an \(N\)-ball is given by

\[V_{2k} = \frac{(\pi r^2)^k}{k!}\]

For both integer and half-integer \(k\). Examples:

\[\begin{aligned} V_0(r) &= \frac{1}{0!} &=& \, 1 \\ V_1(r) &= \frac{(\pi r^2)^{1/2}}{(\frac{1}{2})!} &=& \, 2 r \\ V_2(r) &= \frac{\pi r^2}{1!} &=& \, \pi r^2 \\ V_3(r) &= \frac{(\pi r^2)^{3/2}}{(\frac{3}{2})!} &=& \, \frac{4}{3} \pi r^3 \\ V_4(r) &= \frac{(\pi r^2)^2}{2!} &=& \, \frac{1}{2} \pi^2 r^4 \end{aligned}\]

This is notable because it is is pretty much the formula for the volume \(T_k(a)\) of a \(k\)-dimensional triangle (i.e. a \(k\)-simplex) with side-lengths \(a\): point, line segment, right triangle, right tetrahedron, etc.

\[T_k(a) = \frac{a^k}{k!}\]

Except that it also gives meaning to evaluating this volume at half-dimensions, for \(a = \pi r^2\):

\[T_k(\pi r^2) = V_{2k}(r)\]

This seems to hint at what’s going on. Nature’s answer to

“How do you find a shape which lies halfway between a triangle and a tetrahedron?”

appears to be:

“Regard the triangle as a \(4\)-ball and the tetrahedron as a \(6\)-ball; then there is a \(5\)-ball halfway between, which can thought of as being a sort of squared \(3/2\)-ball.”

Which is at least a little bit concrete.

Here’s a way of thinking about what’s going on. One possible set of constraints to describe a right tetrahedron with side lengths \(a\) is

\[\begin{aligned} 0 < x, y, z &< a \\ x + y + z &< a \end{aligned}\]

The volume integral over this is

\[T_3(a) = \int_0^a \int_0^{a-z} \int_0^{a-y-z} \d x \d y \d z = \frac{a^3}{3!}\]

The factor \(1/3!\) here indicates that inside the volume \([0,a]^3\) there are six total tetrahedrons, of which we have described one. The precise number is easier to see if you change the coordinates such that our tetrahedron is described by \(0 < x' < y' < z' < a\), via \((x',y',z') = (x, x+y,x+y+z)\). Then there is clearly one tetrahedron for each possible ordering of \((x',y',z')\), hence \(3! = 6\) total inside the volume, and we can write \(\int_{[0,a]^3} dV = 3! \cdot T_3(a)\). (This the same procedure as when you split an integral based on the even/odd-ness of an integrand (e.g. \(\int_{-a}^a \cos(x) \d x = 2 \int_0^a \cos(x) \d x\)), but the factorization is over a slightly more complicated symmetry.)

Now suppose we are thinking of the same tetrahedron as “actually” being a \(6\)-ball, whatever that means. We regard \(x+ y + z < a\) as describing the relatinoship between the areas of three circles with radii \((r_x, r_y, r_z)\), whose overall radius is constrained to be less than \(R = \sqrt{a/\pi}\)

\[\begin{aligned} 0 \leq \pi r_1^2 + \pi r_2^2 + \pi r_3^2 < \pi R^2 \end{aligned}\]

And we can expand this into the six coordinates, with each radius living in its own plane. Call these coordinates \((x_1, x_2)\), \((y_1, y_2)\), and \((z_1, z_2)\):

\[\begin{aligned} 0 \leq x_1^2 + x_2^2 + y_1^2 + y_2^2 + z_1^2 + z_2^2 &< R^2 \\ \end{aligned}\]

This of course describes a \(6\)-ball. The volume is

\[V_6(R) = \frac{(\pi R^2)^3}{3!} = V_6(\sqrt{a/\pi}) = \frac{a^3}{3!} = T_3(a)\]

Here are a few ways to expand it as an integral:

\[\begin{aligned} V_6(R) &= \int_0^{\pi R^2} \int_0^{\pi R^2-z} \int_0^{\pi R^2-z-y} \d x \d y \d z \\[1em] &= \int_0^{\pi R^2} \int_0^{\pi R^2 - \pi r_3^2} \int_0^{\pi R^2 - \pi r_3^2 - \pi r_2^2} \d V_2(r_1) \d V_2(r_2) \d V_2(r_3) \\[1em] &= \int_0^R \int_0^{R - r_3} \int_0^{R - r_3 - r_2} (2 \pi dr_1) (2 \pi dr_2) (2 \pi dr_3) \\ &= \int_0^R \int_0^{\sqrt{R^2 - z_2^2}} \int_0^{\sqrt{R^2 - z_2^2 - z_1^2}} \int_0^{\sqrt{R^2 - z_2^2 - z_1^2 - y_2^2}} \int_0^{\sqrt{R^2 - z_2^2 - z_1^2 - y_2^2 - y_1^2}} \\[1em] &\mskip{7em}\int_0^{\sqrt{R^2 - z_2^2 - z_1^2 - y_2^2 - y_1^2 - x_2^2}} \d x_1 \d x_2 \d y_1 \d y_2 \d z_1 \d z_2 \end{aligned}\]

I found it somewhat enlightening to sit and contemplate how all of these can mean the same thing despite the fact that we started out describing a tetrahedron.

Anyway, the Gamma function tells us that the interpolation between \(T_2(a)\) and \(T_3(a)\) looks like removing one of the internal coordinates of one of these circles: it’s a figure defined by, say, \(0 \leq x_1^2 + x_2^2 + y_1^2 + y_2^2 + z_1^2 < R^2\), with no \(z_2^2\) term. I guess it might be helpful to picture a tetrahedron with three sides of length \(\pi R^2\)… and then imagine “square-rooting” one of them, getting two and a half sides? Which sounds absurd except that \(\Gamma\) is telling us that it’s not. Weird.

To draw something like this, I like to draw a figures with doubled lines to represent when a single direction is referring to multiple “internal” dimensions. So the relationship we’re positing might be illustrated as

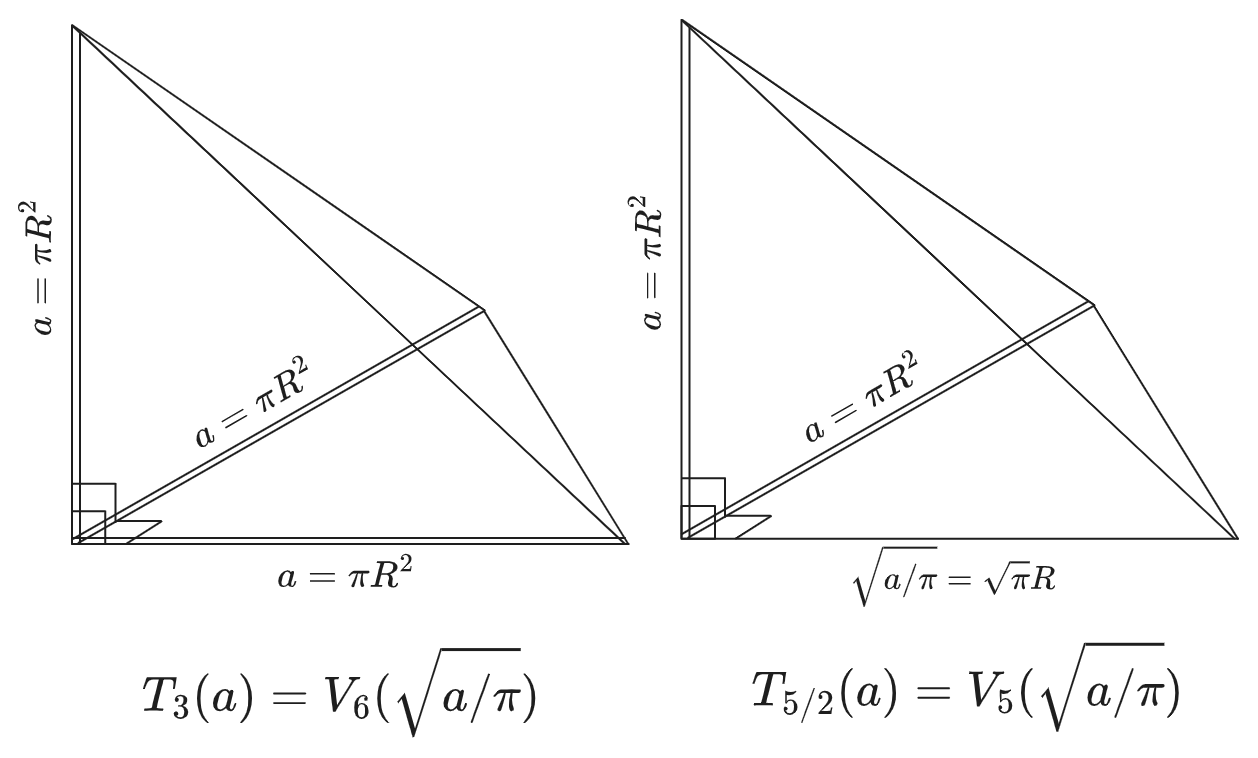
Can’t tell you why it holds but nature seems to say it does in some sense. (This way of drawing is useful for graphing vectors over a “multibasis”, such as the \((x, yz)\) plane.)

---

We can invert the formula for \(V_{2k}\) into something which gives a “definition” of the factorial in terms of the volume:

\[\begin{aligned} k! &= \frac{T_k(a)}{a^k} = \frac{V_{2k}(r)}{(\pi r^2)^k} = \frac{V_{2k}(r)}{V_2(r)^k} \end{aligned}\]

Maybe we simplify now by dropping the radial factors. After all the factorial is only really describing the dimensionality of the space, how many permutations of its axes there are, and the radii only serve to turn this into a volume. With \(T_k = T_k(1)\) and \(V_{2k} = V_{2k}(1)\),

\[k! = T_k = \frac{V_{2k}}{\pi^k} = \frac{V_{2k}}{V_2^k}\]

The first equality is perfectly agreeable: for integer \(k\), the factorial is the number of permutations of \(k\) directions in space, equivalent to the permutations of \(k\) elements. The others are still weird. A \((2k)\) ball also has \(2k\) “axes”, but somehow, by dividing by \(\pi^k\), they only have \(k!\) symmetry, instead of \(2k\)? Or maybe a better way of putting it is: if you want to locate \((\frac{5}{2})!\) between \(2!\) and \(3!\), you can double both dimensions and treat them as symmetries of squares… but you have to rescale \(a \mapsto \pi r^2\) to keep everything having the same volume.

One attempt at a combinatoric interpretation might be: suppose we had a list which appeared to us to contain three elements \((x,y,z)\), but each element was “actually” a label for two elements, so the list is really \((x_1, x_2, y_1, y_2, z_1, z_2)\), with \(6!\) permutations.² We can trivially recover the sense of there being \(3!\) permutations by demanding that the elements stay in pairs: \(((x_1, x_2), (y_1, y_2), (z_1, z_2))\), where the permutations keep each pair together. But the above formula suggests that this is not what’s happening: in \(k! = V_{2k}/\pi^k\), all six internal elements are really treated symmetrically in the “permutation”. Permuting pairs produces \((2k)!!\), not \(k!\), and doesn’t have any interpretation on an odd number of elements.

The only way I can imagine making actual sense of a formula like that is if we can think of a geometric space in which it is actually the case. That would be some situation in which \(S_k\), the symmetric group on \(k\) elements, can be identified perhaps with a quotient \(D^{2k}/(D^2)^k\), where \(D^n\) is an \(n\) disk (the interior of an \(n\)-ball), and then our equation is expressing its volume.

Actually, turns out that’s a thing: the symmetric product \(\text{Sym}^n(X)\) of a topological space. I regret that I know almost nothing about topology, but the basic idea is pretty straightforward:

Starting from a space \(X\), one constructs the space \(\text{Sym}^n(X)\) which takes \(n\) points from \(X\) and then forgets their ordering via the quotient \(X^n/S_n\) (with \(S_n\) being the symmetric group on \(n\) elements). For example, \(\text{Sym}^k(I)\) where \(I\) is the unit interval \([0,1]\) consists of sets of \(n\) points from the unit interval without ordering. Then each equivalence class can be identified by sorting the points. This describes the \(k\)-simplexes: it is exactly the construction we saw for the volume of a tetrahedron above.

An LLM informs me that in the case where \(X = D^2\), the \(2\)-disc (that is, the interior of the \(2\)-ball). Then \(D^2\) turns out to have symmetric product

\[D^{2k} = \text{Sym}^k(D^2) = \frac{(D^2)^k}{S_k}\]

That is: the \(2k\)-disc (which has volume \(V_{2k}\)) is exactly what you get if you quotient \(k\) copies of of the \(2\)-disc (with volume \(V_2\)) by the symmetric group on \(k\) elements.

I have no idea how valid to take a “volume” of this, but since \(V^{2k} = V_2^k/k!\) holds, I’m assuming it works in some sense. (Despite this the construction is not as simple as it looks. Apparently the boundary of this turns out to be \(\p \text{Sym}^k(\p D^2) = \text{Sym}^k(S^1) \cong S^1\) rather than \(\p D^{2k} = S^{2k-1}\), so the sense of “equivalence” here is a bit subtle.)

Here then are two natural questions that I’m also not equipped to answer:

1. Can we make sense of \(D^{2k-1} = (D^2)^{k-1/2} / S_{k-1/2}\) somehow? What would it mean to talk about the product of \((k-1/2)\) copies of \(D^2\) in the symmetric product?
2. Can we “invert” this somehow to describe the symmetry group as \(S_k = (D^2)^k/D^{2k}\)?, giving something that acts like a permutation group but is defined at half-integers?

For (2), the LLM suggests that you can extract \(S_k\) from the spaces by thinking of it as the deck transformation group (not a great name) of the covering given by \((D^2)^k\) over \(D^{2k}\). I haven’t found any reference which suggests that this respects volumes, but I don’t see why it wouldn’t. But still we would need to make it make sense on half-integers.

We’ll stop this line of investigation there since I don’t know enough about topology to continue. Let me do a few years of grad school and get back to you. Anyway, even if it works, it only gets you values of \(S_{n/2}\), not any other fractions, so we will need to keep looking for a way to produce larger denominators.

---

2. The \(k=1/4\) Case

Now we look for an equivalent formula to \(V_{2k}(r) = V_2(r)^k/k!\) that involves \((\frac{1}{4})! = \frac{1}{4} \Gamma(\frac{1}{4})\) instead. From the earlier discussion we can say that the reason the volume \(2k\)-balls looks like the volume of \(k\)-simplexes is because their constraint

\[\begin{aligned} x_1^2 + y_1^2 + x_2^2 + y_2^2 + \ldots + x_k^2 + y_k^2 < R^2 \end{aligned}\]

Can be regarded as a linear equation in the volume of each pair of variables

\[\begin{aligned} \vol(x_1^2 + y_1^2)/\pi + \vol(x_2^2 + y_2^2)/\pi + \ldots + \vol(x_k^2 + y_k^2)/\pi &< R^2 \\ \end{aligned}\]

And then these obey permutation symmetry. because they’re a list of identical linear factors that add up to a constant:

\[(\pi r_1^2) + (\pi r_2^2) + \ldots + (\pi r_k^2) < \pi R^2\]

That is,

\[a_1 + a_2 + \ldots + a_k = a\]

(There are presumably many other ways to describe the same property; this is just one that I find easy to think about.)

The fact that this interpolates to half-integers by removing one factor like \(z_1^2\) is still a bit miraculous. But anyway, the critical feature here is that the volume of a pair of terms \(x_1^2 + y_1^2\) is proportional to their sum: if \(x_1^2 + y_1^2 = r_1^2\), then \(\vol(x_1^2 + y_1^2 < r_1^2) = \pi r_1^2\).

It seems clear that to get a \(1/4\) interpolation we want an expression which groups factors four at a time instead of two, such that the volume of four terms is proportional to their sum, and then we can try removing three terms to produce a “\(1/4\)” permutation.

A first guess would be to try using the \(4\)-disc instead of the \(2\)-disc? But this doesn’t work. The volume of

\[w^2 + x^2 + y^2 + z^2 = R^2\]

is \(V_4(R) = \frac{1}{2} \pi^2 R^4\), which is not proportional to the sum of the four values. If it was going to work, we would be able to summarize a list of \(4k\) coordinates into \(k\) copies of \(4\)-discs, e.g. \(\sum_{i=1}^8 x_i^2 = V_4(r_1) + V_4(r_2) \? V_4(R)\). Then the volume would be \(V_8(R) \? V_4(R)^2/2!\) and would correspond to an integral

\[V_8(R) \? \int_0^{V_4(R)} \int_0^{V_4(R) - V_4(r_2)} \d V_4(r_1) \d V_4(r_2)\]

But that’s not the case: we know that \(V_8(R) = (\pi R^2)^4/4! = \frac{1}{3!} V_4(R)^2\), not \(\frac{1}{2} V_4(R)^2\). The problem is that \(V_4(r_1) + V_4(r_2) \neq V_4(R)\): Each term expands like \(V_4(r_1) = \frac{1}{2} \pi^2 r_1^4 = \frac{1}{2} \pi^2 (x_1^2 + x_2^2 + x_3^3 + x_4^2)^2\), and there are a bunch of cross terms so the pair does not add up to \(\frac{1}{2}\pi^2 R^4\).

What we need to do instead is consider a figure defined by fourth powers:

\[w^4 + x^4 + y^4 + z^4 < S^4\]

These are the “\(n\)-balls in other norms” (ref). In this case the \(L_4\) norm \(\| x \| = \sqrt[4]{\sum x_i^4}\). The volume should now be proportional to \(S^4\), since it defines a four-dimensional figure, although I don’t know the proportionality constant without looking it up. However, we can try to figure it out.

Suppose we define \(W_4(S) = cS^4\) to be the volume of the region satisfying that constraint, where \(c\) is a constant akin to \(\pi\) that we don’t know yet. Then we postulate that a similar formula will hold as for spheres:

\[W_{4k}(S) \? \frac{W_4(S)^k}{k!}\]

And this is trivially the case for integer \(k\), since the constraint is equivalent to

\[c \sum_{i=1}^k x_{i1}^4 + x_{i2}^4 + x_{i3}^4 + x_{i4}^4 = \sum_{i=1}^k cs_k^4 = \sum_{i=1}^k W_4(s_i) = cS^4\]

For example,

\[x_1^4 + x_2^4 + x_3^4 + x_4^4 + y_1^4 + y_2^4 + y_3^4 + y_4^4 = cW_4(s_1) + cW_4(s_2) < cS^4\]

Which puts it in the same linear form as for the spheres and gives the volume \(W_{4k}(S) = W_4(S)^{k}/k!\).

To find the value of \(c\) we could try integrating over four variables, which is hard, or we can assume that our interpolation formula works and plug in \(k=1/2\). Then the constraint is

\[x^4 + y^4 < S^4\]

Which has volume given by the integral

\[\begin{aligned} \text{vol}(x^4 + y^4 < S^4) &= 4 \int_0^S \sqrt[4]{S^4 - x^4} \d x \\ &= 4 S^2 \int_0^1 \sqrt[4]{1-x^4} \d x \\ \end{aligned}\]

We can find this among the identities for the lemniscate constant (ref), which afterall is just a name given to the volume of a particular region, which can be defined by an integral. Just like \(\pi\) could be defined by \(\pi \equiv 4 \int_0^1 \sqrt{1-x^2} dx\), it turns out that \(\varpi = 2 \sqrt{2} \int_0^1 \sqrt[4]{1-x^4} \d x\), so

\[\text{vol}(x^4 + y^4 < S^4) = 4S^2 \frac{\varpi}{2 \sqrt{2}} = \sqrt{2} S^2 \varpi\]

(Note: the actual lemniscate figure is a different shape, defined by \((x^2 + y^2)^2 = x^2 - y^2\), with volume \(2 \varpi\), and so everything involving \(\varpi\) has a weird constant in fron it. But its volume is related to ours. Both geometries involve fourth powers and I suppose the simple proportionality factor implies that they are connected by a simple change-of-variables.)

Assuming our interpolation \(W_{4k}(S) = W_4(S)^k/k!\) is true at multiples of \(1/4\), then

\[W_2(S) = \frac{W_4(S)^{1/2}}{(\frac{1}{2})!} = \frac{\sqrt{c} S^2}{\frac{1}{2} \sqrt{\pi}} = \sqrt{2} S^2 \varpi\]

Which gives the value of \(c\) as

\[c = \frac{1}{2} \pi \varpi^2\]

And the volume of \(W_{4k}(S)\) as

\[W_{4k}(S) = \frac{[\frac{1}{2} \pi \varpi^2 S^4]^{k}}{k!}\]

Which is the \(W\)-version of \(V_{2k}(R) = (\pi R^2)^k / k!\).

Now we check \(W_1 \equiv W_1(1)\), which must equal \(2\) since that is the volume of \(x^4 < 1\), to get the interpolated value of \(\Gamma(\frac{1}{4})!\)

\[\begin{aligned} W_1 &= \frac{W_4^{1/4}}{(\frac{1}{4})!} \\ 2 &= \frac{\sqrt[4]{c}}{\frac{1}{4} \Gamma(\frac{1}{4})} \\ \Gamma(\frac{1}{4}) &= 2 \sqrt[4]{\frac{1}{2} \pi \varpi^2} \\ &= \sqrt[4]{8\pi \varpi^2} \\ &= \sqrt{2 \varpi \sqrt{2 \pi}} \end{aligned}\]

Which is correct. We can also double-check our calculation of \(W_2\):

\[W_2 = \frac{W_4^{1/2}}{(\frac{1}{2})!} = \frac{\sqrt{\frac{1}{2} \pi \varpi^2}}{\frac{1}{2} \sqrt{\pi}} = \sqrt{2} \varpi\]

As expected.

Since \(V_{2k}(R) = T_k(\pi R^2)\), we have

\[\begin{aligned} W_{4k}(S) &= T_k(\frac{1}{2} \pi \varpi^2 S^4) \\ &= V_{2k}(\frac{1}{\sqrt{2}} \varpi S^2) \end{aligned}\]

Therefore we can write \(V_{2k}(R) = W_{4k}(\sqrt{\sqrt{2} R/\varpi})\). For instance \(W_2(\sqrt{\sqrt{2} R/\varpi}) = W_2(1) (\sqrt{\sqrt{2} R/\varpi})^2 = 2R = V_1(R)\). So \(W_k(\sqrt{\sqrt{2} R/\varpi})\) is producing the volumes of spheres in a way that interpolates to half-integers, whatever that means.

---

This seems to lend some credence to this sense of interpolation: we picked \(W_4\) based on the pattern set by \(V_2\) and came up with the right answer with a (relatively) simple argument. Not a proof, but I think it’s pretty convincing. It seems clear that what we did here should work for any \(L_p\) norm: to interpolate to \((1/k)!\), define the figure \(x_1^k + x_2^k + \ldots x_k^k < R^k\) and then extrapolate to non-integer values. Not that there’s any new material here; it’s just a rephrasing of what we already know about \(\Gamma\). But I think this way of proceeding through things sheds some light on what’s going on, and I haven’t seen anything like this really described anywhere else (everyone seems very nervous about trying to literally talk about permutations of fractional dimensions since they seem so nonsensical). Apparently:

1. To construct half-integer permutations, we interpolate sets of \(k\) elements with balls of \(2k\)-dimensions
2. To construct quarter-integer permutations, we interpolate those \((2k)\)-balls with \((4k)\)-\(L_4\)-balls (whatever you call those).
3. Presumably this continues to hold for all the other rationals: \(V^{ab}\) balls are used to interpolate \(b\) values between each of the \(V^a\) balls.
4. Indeed, the regular permutations \(n!\) at integers may be seen as (proportional to) the volumes of \(L_1\)-balls, which are defined by \(\| x \| = \sum \| x_i \| < R\) and are therefore given by copies of standard simplexes rotated around the origin. (Specifically, \(n!! = 2^n n!\) is \(L_1\)-ball in \(n\) dimensions, since the ball is within \([-1,1]^n\) instead of \([0, 1]^n\).)

Writing \(V_n^p\) for the volume of a unit \(n\)-ball in the \(p\)-norm, we extrapolate to a formula for all rationals \(m/k\):

\[V_{m}^k =\frac{(V^k_k)^{m/k}}{(\dfrac{m}{k})!}\]

Since in all norms the \(1\)-ball has volume \(2\), we can write

\[\begin{aligned} 2 = V^k_1 &= \frac{\sqrt[k]{V^k_k}}{(\dfrac{1}{k})!} \\ V^k_k &= (2 (\dfrac{1}{k})!)^k \\[1.5em] \end{aligned}\]

Giving the general \(V^k_m\) volume as

\[V_m^k = \frac{ (2 (\dfrac{1}{k})!)^{m/k}}{(\dfrac{m}{k})!}\]

And conversely the factorial as

\[(\frac{m}{k})! = \frac{ (2 (\dfrac{1}{k})!)^{m/k}}{V_m^k} = \frac{(V^k_k)^{m/k}}{V_m^k}\]

These relations are all well-known (see Wikipedia or this SE question); I just like my way of finding them. For completeness let me mention anentirely different way of reaching this formula, which is to start from \(\Gamma(x) = \int_0^{\infty} t^{x-1} e^{-t} \d t\). First substitute \(t=y^{1/x}\), then evaluate at \(1+1/k\) and use the same \(I^2 = \pi\) trick as for solving the Gaussian, but for an \(L_k\) volume instead:

\[\begin{aligned} \Gamma(x) &= \int_0^{\infty} t^{x-1} e^{-t} \d t \\ &= \int_0^{\infty} y^{(x-1)/x} e^{-y^{1/x}} \frac{1}{x} y^{(1-x)/x} \d y \\ \Gamma(1+x) &= \int_0^{\infty} e^{-y^{1/x}} \d y \\ \Gamma(1+\frac{1}{k}) &= \int_0^{\infty} e^{-y^k} \d y \\ \Gamma(1+\frac{1}{k})^k &= \frac{1}{2^k} \int_{\bb{R}^k} e^{-y_1^k - y_2^k - \ldots - y_k^k} \d y\\ &= \frac{1}{2^k} V^k_k \int_{0}^{\infty} r^{k-1} e^{-r^k} \d r \\ (\frac{1}{k})!^k &= \frac{1}{2^k} V^k_k \end{aligned}\]

One other interesting form follows from the fact that we know how to write \(V_2^k\) as an integral:

\[V_2^k = 4 \int_0^1 \int_0^{\sqrt[k]{1-x^k}} \d y \d x = \int_0^1 \sqrt[k]{1 - x^k} dx\]

Which after plugging into \(V_2^k = (V_k^k)^{2/k} / (\frac{2}{k})!\) gives

\[\begin{aligned} [\int_0^1 \sqrt[k]{1 - x^k} dx] \times (\frac{2}{k})! &= (\dfrac{1}{k})!^{2} \end{aligned}\]

Showing that the algebraic relationship between \((1/k)!\) and \((2/k)!\) is non-trivial, involving the value of this integral. Similar arguments would work for \(V_3^k = 2^3 \int_0^1 \int_0^{\sqrt[k]{1-z^k}} \int_0^{\sqrt[k]{1-z^k-y^k}} \d x \d y \d z\), etc, but I don’t want to try to write them all out.

Suffice to say, the general relationship between \((\frac{a}{k})!\) and \((\frac{a+1}{k})!\) is nested integration. Maybe that works as a concise explanation of why the values of the factorial function are so complicated. It also gives way of making sense why \(\Gamma\) shows up in the fractional calculus: \(\p_x^{-2} f(x) = \int \int f(x) \d x \d x\) was already a nested integral; turns out when you fractionalize \(\p_x\) you have to split each single integral into more integrals to do it; in fact the factorial is interpolating between integers in the same way.

---

So far I can’t tell if there’s any way to derive any new relationships from this way of looking at things. My guess is no: I think what we’re doing here is using a geometric interpretation in order to manipulate the integral form of \(\Gamma\) indirectly. But I thought it was an interesting way of doing things, which at least I have not come across anywhere else. It really is saying something about what comes “in between” integer permutations, at least in the specific interpolation of \(n!\) which is alluded to by the Gamma functiom.

My curiosity about this was in the first place piqued when I was searching for answers to questions like “is it possible to interpret \(\Gamma\) at non-integers as some kind of fractional permutation?” And almost everything you find in response is some sort of “no-go” reply (e.g. on StackExchange): arguments of the form, “based on what a dimension is, no”. Perhaps with some vague nod to fractals that can exhibit qualities akin to non-integer dimension. I’ve always found those answers to be somewhat close-minded and unimaginative. Not that I have the answer myself, but isn’t it pretty clear there’s something concrete going on here? \(\Gamma\) is not “just” an interpolation; there’s far too much structure for that. There is some valid notion of fractional permutations, fractional sets, fractional spheres, etc in which these concepts are going to make sense.

A good thing to do next would be to look at some examples of how fractional factorials actually arise and see if we can locate the interpolating spherical geometry within them. But I don’t have any good ideas, yet. I’d also like to try to make sense of the interpolations at negative or imaginary numbers, since \(\Gamma\) is well-defined at most of those. I expect that even the negative integers have a concrete meaning waiting to be found.